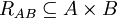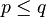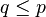studentsite

studentsite
studentsite

Senin, 23 Juni 2014

contoh soal

1.Misalnya ada sebuah contoh soal Relasi
"1 Kurangnya Dari", dan Domainnya adalah A={0,1,2,3,4}
Kodomainnya adalah B={1,2,3,4,5}
Maka Rangenya adalah R={(Domain,Kodomain)}--> R={(0,1)(1,2)(2,3)(3,4)(4,5)}
Dibacanya R={(0 satu kurangnya dari 1) (1 satu kurangnya dari 2) 
2. Perhatikan diagram panah di bawah ini.
A → B
2 → 3
3 → 4
4 → 5
5 → 6
Relasi yang tepat dari himpunan A ke himpunan B adalah... ?
A. Lebih dari
B. Kurang dari
C. Satu lebihnya dari
D. Satu kurangnya dari

3. Suatu fungsi dirumuskan f(x) = 9 - 3x. Jika f(p) = 15, nilai p adalah... ?
A. -8
B. -2
C. 2
D. 8
jwb :
f(x) = 9 - 3x
dari soal diatas kita cuma diperintahkan untuk mensubstitusikan p ke dalam x, sehingga :
f(x) = 9 - 3x
f(p) = 9 - 3p
karena f(p) = 15, maka kita substitusikan 15 ke dalam f(p).
f(p) = 9 - 3p
15 = 9 - 3p
15 - 15 = 9 - 3p -15
0 = 9 - 15 - 3p
0 + 3p = 9 - 15 - 3p + 3p
3p = - 6 + 0
p = -6 / 3
p = -2.
jadi nilai p adalah -2.

Diposting oleh di Tidak ada komentar:

Domain,kodomain dan Range


Domain adalah himpunan asal yang dipetakan dalam fungsi
Kodomain adalah himpunan tujuan pemetaan dalam fungsi
Range adalah daerah hasil pemetaan yang merupakan bagian dari kodomain.

Diposting oleh di Tidak ada komentar:

Perbedaan Funsi dan Relasi


Relasi, dalam matematika, adalah hubungan antara dua elemen himpunan. Hubungan ini bersifat abstrak, dan tidak perlu memiliki arti apapun baik secara konkrit maupun secara matematis.
Jika terdapat himpunan A dan himpunan B (A bisa sama dengan B), maka relasi R dari Ake B adalah subhimpunan dari A×B.
R_{AB} \subseteq A \times B

 RELASI DAN FUNGSI PROPOSISI

Sebuah relasi dapat dikaitkan dengan sebuah fungsi proposisi atau kalimat terbuka yang himpunan penyelesaiannya tidak lain adalah relasi tersebut.
Sebagai contoh, pandang himpunan B = { apel, jeruk, mangga, pisang } dengan himpunan W = { hijau, kuning, orange}. Suatu relasi R dari A ke B didefinisikan sebagai R= {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}. Terdapat fungsi proposisi w(x, y) = "x berwarna y", yang himpunan penyelesaiannya adalah {(apel, hijau), (jeruk, orange), (mangga, hijau), (pisang, kuning)}, yang tidak lain adalah relasi R.

 

RELASI A×A

Sebuah relasi A×A, yaitu relasi dari himpunan A kepada A sendiri, dapat memiliki sifat-sifat berikut:
  • Refleksif
  • Irefleksif
  • Simetrik
  • Anti-simetrik
  • Transitif
Kita menyebut relasi R dari A kepada A sebagai relasi R dalam A.

 Relasi Refleksif

Sebuah relasi R dalam A disebut memiliki sifat refleksif, jika setiap elemen Aberhubungan dengan dirinya sendiri.
\forall_{a \in A}\quad (a,a) \in R
atau
\forall_{a \in A}\quad a R a
Contoh relasi yang memiliki sifat seperti ini adalah relasi “x selalu bersama y.”, dengan xdan y adalah anggota himpunan seluruh manusia. Jelas sekali bahwa setiap orang pasti selalu bersama dengan dirinya sendiri.


 Relasi Irefleksif

Relasi R dalam A disebut memiliki sifat irefleksif, jika setiap elemen A tidak berhubungan dengan dirinya sendiri.
\forall_{a \in A}\quad (a,a) \notin R
atau
\forall_{a \in A}\quad \lnot(a R a)
Contoh relasi irefleksif adalah relasi “x mampu mencukur rambut y dengan rapi sempurna.”, dengan x dan y adalah setiap pemotong rambut. Diandaikan bahwa setiap orang hanya dapat mencukur rambut orang lain dengan rapi sempurna, maka relasi ini adalah irefleksif, karena tidak ada seorang tukang cukur a yang mampu mencukur rambutnya sendiri.
Contoh lain dalam himpunan bilangan bulat adalah, relasi < dan > adalah irefleksif.


 Relasi Simetrik

Relasi R dalam A disebut memiliki sifat simetrik, jika setiap pasangan anggota Aberhubungan satu sama lain. Dengan kata lain, jika a terhubung dengan b, maka b juga terhubung dengan a. Jadi terdapat hubungan timbal balik.
\forall_{a, b \in A}\quad (a,b) \in R \rightarrow (b,a) \in R
atau
\forall_{a, b \in A}\quad a R b \rightarrow b R a
Sebuah relasi “x + y genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.


Relasi Anti-simetrik

Jika setiap a dan b yang terhubung hanya terhubung salah satunya saja (dengan asumsia dan b berlainan), maka relasi macam ini disebut relasi anti-simetrik.
\forall_{a, b \in A}\quad a \neq b \rightarrow ((a,b) \in R \rightarrow (b,a) \notin R)
atau
\forall_{a, b \in A}\quad a \neq b \rightarrow (a R b \rightarrow \lnot (b R a))
Dalam kebanyakan literatur biasanya ditulis sebagai kontraposisinya seperti di bawah ini. Keuntungan bentuk ini adalah tidak mengandung negasi, dan hanya mengandung satu implikasi.
\forall_{a, b \in A}\quad (a,b) \in R \wedge (b,a) \in R \rightarrow a=b
atau
\forall_{a, b \in A}\quad a R b \wedge b R a \rightarrow a=b
Relasi \leq bersifat anti-simetrik, karena 5 \leq 6 mengakibatkan \lnot (6 \leq 5). Demikian juga jika ada p dan q yang terhadap mereka berlaku p \leq q dan q \leq p berarti p = q.


 Relasi Transitif

Sebuah relasi disebut transitif jika memiliki sifat, jika a berhubungan dengan b, dan bberhubungan dengan c, maka a berhubungan dengan c secara langsung.
(a,b) \in R \wedge (b,c) \in R \rightarrow (a,c) \in R
atau
\forall_{a, b, c \in A} {a R b \wedge b R c \rightarrow a R c}
Sebagai contoh, relasi dua transitif. Misalnya untuk 5, 6, dan 7, berlaku 5 < 6, 6 < 7, dan 5 < 7.

 RELASI KHUSUS

 Relasi Ekivalen

Sebuah relasi disebut sebagai relasi ekivalen jika relasi tersebut bersifat:
  • Refleksif
  • Simetrik, dan
  • Transitif
Relasi ekuivalen memiliki hubungan erat dengan partisi, yang merupakan alasan mengapa partisi dari sebuah himpunan disebut kelas ekivalen atau kelas kesetaraan.


 Orde Parsial

Orde parsial adalah relasi yang bersifat:
  • Refleksif
  • Anti-simetrik, dan
  • Transitif


Fungsi (matematika)

Fungsi, dalam istilah matematika adalah pemetaan setiap anggota sebuah himpunan(dinamakan sebagai domain) kepada anggota himpunan yang lain (dinamakan sebagai kodomain). Istilah ini berbeda pengertiannya dengan kata yang sama yang dipakai sehari-hari, seperti “alatnya berfungsi dengan baik.” Konsep fungsi adalah salah satu konsep dasar dari matematika dan setiap ilmu kuantitatif. Istilah "fungsi", "pemetaan", "peta", "transformasi", dan "operator" biasanya dipakai secara sinonim.
Anggota himpunan yang dipetakan dapat berupa apa saja (kata, orang, atau objek lain), namun biasanya yang dibahas adalah besaran matematika seperti bilangan riil. Contoh sebuah fungsi dengan domain dan kodomain himpunan bilangan riil adalah y=f(2x), yang menghubungkan suatu bilangan riil dengan bilangan riil lain yang dua kali lebih besar. Dalam hal ini kita dapat menulis f(5)=10


NOTASI

Untuk mendefinisikan fungsi dapat digunakan notasi berikut.
f : A \rightarrow B
Dengan demikian kita telah mendefinisikan fungsi f yang memetakan setiap elemen himpunan A kepada B. Notasi ini hanya mengatakan bahwa ada sebuah fungsi f yang memetakan dua himpunan, A kepada B. Tetapi bagaimana tepatnya pemetaan tersebut tidaklah terungkapkan dengan baik. Maka kita dapat menggunakan notasi lain.
x \in A
f : x \rightarrow x^2

Diposting oleh di Tidak ada komentar:

Fungsi dan Relasi

Galileo Galilei (1564-1642) merupakan salah satu astronom terkenal dari Italia yang dikenal luas dengan penemuannya tentang hubungan yang sangat teratur antara tinggi suatu benda yang dijatuhkan dengan waktu tempuhnya menuju tanah.
Konsep “fungsi” terdapat hampir dalam setiap cabang matematika, sehinggamerupakan suatu yang sangat penting artinya dan banyak sekali kegunaannya. Akan tetapi pengertian dalam matematika agak berbeda dengan pengertian dalam kehidupan sehari-hari.Dalam pengertian sehari-hari, “fungsi” adalah guna atau manfaat. Kata fungsi dalam matematika sebagaimana diperkenalkan oleh Leibniz (1646-1716) terlihat di atas digunakan untuk menyatakan suatu hubungan atau kaitan yang khas antara dua himpunan.
Mengingat konsep fungsi menyangkut hubungan atau kaitan dari dua himpunan, maka disini kita awali dulu pembicaraan kita mengenai fungsi dengan hubungan atau relasi antara dua himpunan.
A.Pengertian Relasi
Suatu relasi (biner) F dari himpunan A ke himpunan B adalah suatu perkawanan elemen-elemen di A dengan elemen-elemen di B.
B.Pengertian Relasi
Suatu relasi (biner) F dari himpunan A ke himpunan B adalah suatu perkawanan elemen-elemen di A dengan elemen-elemen di B. didefinisikan sebagai berikut :
Definisi: Suatu fungsi f dari himpunan A ke himpunan B adalah suatu relasi yang memasangkan setiap elemen dari A secara tunggal, dengan elemen pada B.
C.Sifat Fungsi
Dengan memperhatikan bagaimana elemen-elemen pada masing-masing himpunan A dan B yang direlasikan dalam suatu fungsi, maka kita mengenal tiga sifat fungsi yakni sebagai berikut :
1. Injektif (Satu-satu)
Misalkan fungsi f menyatakan A ke B maka fungsi f disebut suatu fungsi satu-satu
(injektif), apabila setiap dua elemen yang berlainan di A akan dipetakan pada dua elemen yang berbeda di B. Selanjutnya secara singkat dapat dikatakan bahwa f:A→B adalah fungsi injektif apabila a ≠ a’ berakibat f(a) ≠ f(a’) atau ekuivalen, jika f(a) = f(a’)
maka akibatnya a = a’.
2. Surjektif (Onto)
Misalkan f adalah suatu fungsi yang memetakan A ke B maka daerah hasil f(A) dari fungsi f adalah himpunan bagian dari B. Apabila f(A) = B, yang berarti setiap elemen di B pasti merupakan peta dari sekurang-kurangnya satu elemen di A maka kita katakan f adalah suatu fungsi surjektif atau “f memetakan A Onto B”.
3.Bijektif (Korespondensi Satu-satu)
Suatu pemetaan f: A→B sedemikian rupa sehingga f merupakan fungsi yang injektif dan surjektif sekaligus, maka dikatakan “f adalah fungsi yang bijektif” atau “ A dan B berada dalam korespondensi satu-satu”
D.Jenis – jenis Fungsi
Jika suatu fungsi f mempunyai daerah asal dan daerah kawan yang sama, misalnya D, maka sering dikatakan fungsi f pada D. Jika daerah asal dari fungsi tidak dinyatakan maka yang dimaksud adalah himpunan semua bilangan real (R). Untuk fungsi-fungsi pada R kita kenal beberapa fungsi antara lain sebagai berikut.
a. Fungsi Konstan
b. Fungsi Identitas
c. Fungsi Linear
d. Fungsi Kuadrat
e. Fungsi Rasiona
Diposting oleh di Tidak ada komentar:

Diagram Ven dan contoh


Diagram Venn pertama kali diketemukan oleh John Venn, seorang ahli matematika dari Inggris yang hidup pada tahun 1834–1923. Dalam diagram Venn,himpunan semesta dinyatakan dengan daerah persegi panjang, sedangkan himpunan lain dalam semesta pembicaraan dinyatakan dengan kurva mulus tertutup sederhana dan noktah-noktah untuk menyatakan anggotanya.

Agar Anda dapat memahami cara menyajikan himpunan dalam diagram Venn, pelajari uraian berikut.
Diketahui:
S = {0, 1, 2, 3, 4, ..., 9};
P = {0, 1, 2, 3, 4}; dan
Q = {5, 6, 7}
Himpunan S = {0, 1, 2, 3, 4, ..., 9} adalah himpunan semesta (semesta pembicaraan). Dalam diagram Venn, himpunan semesta dinotasikan dengan S berada di pojok kiri.

Perhatikan himpunan P dan Q. Karena tidak ada anggota persekutuan antara P dan Q, maka PΛQ = { }. Jadi, dapat dikatakan bahwa kedua himpunan saling lepas. Dalam hal ini, kurva yang dibatasi oleh himpunan P dan Q saling terpisah.

Selanjutnya, anggota-anggota himpunan P diletakkan pada kurva P, sedangkan anggota-anggota himpunan Q diletakkan pada kurva Q. Anggota himpunan S yang tidak menjadi anggota himpunan P dan Q diletakkan di luar kurva P dan Q. Diagram Venn-nya seperti Gambar 6.4 di bawah ini.




Contoh Soal Tentang Diagram Venn 
Diketahui S = {1, 2, 3, ..., 10} adalah himpunan semesta (semesta pembicaraan), A = {1, 2, 3, 4, 5}, dan B = {bilangan genap kurang dari 12}. Gambarlah dalam diagram Venn ketiga himpunan tersebut.

Penyelesaian:
Diketahui:
S = {1, 2, 3, ..., 10}
A = {1, 2, 3, 4, 5}
B = {2, 4, 6, 8, 10}
Berdasarkan himpunan A dan B, dapat diketahui bahwa AΛB = {2, 4}. Perhatikan bahwa himpunan A dan B saling berpotongan. (Mengapa?) Dalam diagram Venn, irisan dua himpunan harus dinyatakan dalam satu kurva (himpunan A dan B dibuat berpotongan). Adapun bilangan yang lain diletakkan pada kurva masing-masing. Diagram Venn-nya sebagai berikut.


Diposting oleh di Tidak ada komentar:

Himpunan dan Contoh


Himpunan adalah kumpulan benda atau objek yang anggota-anggotanya dapat didefisikan dengan jelas. Sedangkan bukan himpunan adalah kumpulan benda \ objek yang anggota-anggotanya tidak dapat terdefisikan dengan jelas.
Contoh kumpulan yang merupakan himpunan :
1. Kumpulan hewan menyusui
Anggotanya dapat ditentukan dengan jelas yaitu kerbau, kambing, sapi, kuda dan lain-lain
2. Kumpulan warna lampu lalu lintas
Anggotanya dapat ditentukan dengan jelas yaitu merah, kuning, hijau.
3. Kumpulan bilangan asli kurang dari 6
Anggotanya dapat ditentukan dengan jelas yaitu 1, 2, 3, 4, 5.
Contoh kumpulan yang bukan himpunan:
1. Kumpulan gadis cantik
2. Kumpulan orang tinggi
3. Kumpulan lukisan yang menarik

Diposting oleh di Tidak ada komentar:

Selasa, 03 Juni 2014

Tingkatan teknologi berdasarkan penerapannya

Teknologi Tinggi ( Hi – tech ). Suatu jenis teknologi mutakhir yang dikembangkan dari hasil penerapan ilmu pengetahuan terbaru. Contoh : computer, laser, bioteknologi, satelit komunikasi dan sebagainya. Ciri – ciri teknologi ini adalah padat modal, didukung rasilitas riset dan pengembangannya, biaya perawatan tinggi, ketrampilan operatornya tinggi dan masyarakat penggunanya ilmiah.
Teknologi Madya. Suatu jenis teknologi yang dapat dikembangkan dan didukung masyarakat yang lebih sederahan dan dapat digunakan dengan biaya dan kegunaan yang paling menguntungkan. Ciri teknologi madya adalah tidak memerlukan modal yang terlalu besar dan tidak memerlukan pengetahuan baru, karena telah bersifat rutin. Penerapan teknologi maday ini bersifat setengah padat modal da padat karya, unsur – unsur yang mendukung industrinya biasanya dapat diperoleh di dalam negeri dan keterampilan pekerjanya tidak terlalu tinggi.
Teknologi Tepat Guna. Teknologi ini dicirikan dengan skala modal kecil, peralatan yang digunakan sederhana dan pelaksanaannya bersifat padat karya. Biasanya dilakukan di negara – negara berkembang, karena dapat membantu perekonomian pedesaan, mengurangi urbanisasi dan menciptakan tradisi teknologi dari tingkat paling sederhana.
Dengan kemajuan pesat ilmu pengetahuan dan teknologi terutama di bidang teknologi informasi dan teknologi transportasi yang dicapai manusia pada unjung pertengahan kedua abad ke XX, memungkinkan arus informasi menjadi serba cepat: apa dan oleh siapa dari seluruh muka bumi (bahkan sebagian jagat raya) – menembus ke seluruh lapisan masyarakat dengan bebas tanpa membedakan siapa dia si penerima. Tanpa mengenal batas jarak dan waktu, negara, ras, kelas ekonomi, ideologi atau faktor lainnya yang dapat menghambat bertukar pikiran. Berikut ini akan dijelaskan mengenai pengaruh perkembangan IPTEK terhadap beberapa pola kemasyarakatan
Diposting oleh di Tidak ada komentar:

Perkembangan IPTEK dimasa kini

Teknologi merupakan instrument utama masyarakat dalam mencapai kesejahteraan melalui penciptaan nilai tambah.kajian mendalam telah menemukan bahwa teknologi sebenarnya merupakan hasil dari suatu proses yang terdiri dari rangkain subproses penelitian dan pengembangan,ivensi,rekayasa dan desain,manufaktur dan pemasaran.disini teknologi diciptakan manusia melalui penerapan budidaya akalnya,teknologi mereka berdasarkan ratio (nalar) dan kemudian membuanya,merekayasanya menjadi suatu produk yang kongkrit.

berkembanganya dengan cepat dan prioritas yang tinggi bagi umat manusia,yaitu material,energi,mikroelektronik dan bioteknologi.

B.PENGARUH PERKEMBANGAN TEKNOLOGI
teknologi kian hari semakin canggih,sehinggah akan membuat kita dituntut untuk memilikinya.keinginan atau hasrat manusia untuk hidup serba instant membuat kita akan terus berfikir dan berusaha untuk mewujudkanya.perkembangan teknbologi pun akan terus berkembang seiring berjalanya waktu,dan kita harus bisamemanfaatkanya dengan sebaik mungkin dan jangan sampai merugikan kita.
      Dalam peradaban manusia,kini teknologi informasi berkembang dengan sangat baik dan dipakai oleh kalangan tertentu tetapi sudah sangat meluas dari lingkungan kota sehingga lingkungan pedesaan,dimana semuanya mungkin sudah dapat mengerti dasar dasar pemakaiannya alat teknologi informasi dengan mudahnya.
Dampak positif:
1.internet sebagai media komunikasi.
2.media pertukaran data.
3.media untuk mencari informasi dan data.

Dampak negatif:
1.mengurangi sifat sosial manusia karena cenderung lebih suka berhubungan lewat internet.
2.pornografi
3.kejahatan menipu dan mencuri dapat melakukanya di internet.

C.PERKEMBANGAN TEKNOLOGI DI INDONESIA
   Di indonesia sebenarnya sudah mulai dengan suatu langkah dan modal yang amat srategis dengan cara menempatkan posisi ilmu pengetahuan dan teknologi sebagai politik negara,yaitu tercantumnya pada pasal 31 ayat 5 UUD 45 ini.intinya adalah,ilmu pengetahuan dan teknologi seharusnya juga menjadi basis pembangunan pemerintah siapapun dan kapan pun di indonesia,sepanjang UUD 45 itu tidak mengalami perubahan.
Diposting oleh di Tidak ada komentar:
Langganan: Postingan (Atom)